Der Markt für Immobilien in Deutschland ist in den letzten Jahren immer heißer geworden. Ich schreibe diesen Artikel im März 2017, und es gibt kaum noch Angebote mit einer Nettomietrendite von über 3%.
Und ja, eine Nettomietrendite ist nicht dasselbe wie die Mietrendite.
Die Mietrendite ist das, was die Makler fett ins Exposé schreiben.
Doch die Nettomietrendite ist das, worauf es am Ende alleine ankommt. Und sie ist „zufällig“ immer etwas niedriger als die Mietrendite.
Ich habe euch schon an anderer Stelle erklärt, was der genaue Unterschied ist, und vor allem wie du ihn (zum Beispiel mit meiner Tabelle) genau berechnen lassen kannst.
Vor 4 Jahren hätte ich mir bei einer Immobilie mit „nur“ 3% Nettomietrendite nicht mal die Mühe einer Besichtigung gemacht.
Doch dieser Tage habe ich mal wieder eine Wohnung gekauft, und ich will euch genau erklären, warum ich trotz einer Nettomietrendite von 2,31% investiert habe, und vor allem warum es trotzdem eine gute Idee ist.
Es handelt sich um eine 1-Zimmer-Wohnung mit 40qm in einer mittelgroßen deutschen Universitätsstadt, die Wohnung liegt sehr zentral und befindet sich in einem soliden Mehrfamilienhaus. Sie kostet 110.000 Euro und ist für 320 Euro Kaltmiete an einen Studenten vermietet.
Natürlich muss ich am Ende mehr bezahlen als nur den Kaufpreis, denn es kommen noch Notargebühren, Grunderwerbsteuer und die Maklercourtage hinzu. Meine Tabelle spuckt dann einen Gesamtpreis von 121.022 Euro aus.
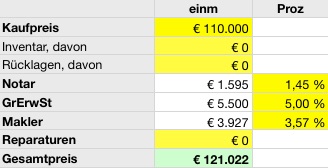
Die Kaltmiete beträgt 320 Euro. Das sind 7,85 Euro pro Quadratmeter, also ein auffallend niedriger Wert. Woher ich das weiß? Also entweder du kennst dich bei den Preisen in der Region aus (das ist bei mir der Fall), oder du googelst nach „Mietspiegel“ und dem Namen der Stadt.
Doch beim Mietspiegel muss du bedenken, dass er den Durchschnittswert der geschlossenen Mietverträge wiedergibt. Aussagekräftiger und für dich viel relevanter ist jedoch der Durchschnittswert der Neuvermietungen. Denn ein vor 10 Jahren geschlossener Mietvertrag beeinflusst zwar den Mietspiegel, doch für eine Neuvermietung ist er irrelevant.
In meinem Fall ist der typische Mietpreis für solche Einzimmerwohnungen in diesem gut gelegenen Stadtteil fast doppelt so hoch wie die hier vereinbarte Miete.
Der erste Gedanke lautet also „Wertsteigerung durch Mieterhöhung“. Doch dazu später mehr. Zuerst rechne ich mit der momentanen Miete weiter.
Für diverse Nebenkosten fällt bei dieser Wohnung ein Hausgeld von etwa 120 Euro im Monat an. Der Mieter bezahlt aber nur 60 Euro Mietnebenkosten. Bleibt also ein nicht umlagefähiger Anteil der Nebenkosten von etwa 720 Euro im Jahr übrig, den ich als Vermieter bezahlen muss,
Für etwaige Reparaturen lege ich zudem immer eine Nettomonatsmiete pro Jahr zurück. Somit komme ich in meiner Tabelle für die Spalte mit den NUF (=nicht umlagefähige Kosten plus Rücklagen) auf 1.040 Euro im Jahr.
Oder anders gesagt reduzieren sich die Netto-Mieteinnahmen damit von 12 x 320 = 3.840 Euro im Jahr auf 2.800 Euro.
Wir haben also einerseits den Kaufpreis von netto auf brutto erhöht, und ich bezahle damit am Ende statt 110.000 Euro mit allen Kaufnebenkosten 121.022 Euro.
Und andererseits haben wir die Mieteinnahmen auf einen Nettobetrag von 2.800 Euro im Jahr reduzieren müssen.
Das zusammen ergibt die Nettomietrendite, also die echte Rendite der Wohnung.
Wenn ein Makler das vorrechnet, dann nimmt er meistens die für ihn günstigeren Zahlen, also die geringeren Kosten und die höheren Einnahmen. Oder in diesem Fall die 110.000 Euro Kosten und 3.840 Euro Einnahmen. Damit käme man auf 3,49% Rendite. Aber diese Zahl ist natürlich Augenwischerei.
Die echten Zahlen von 121.022 Euro Kosten und 2.800 Euro jährliche Einnahmen ergeben vielmehr die Nettomietrendite von 2,31%. Das ist ernüchternd wenig, und selbst eine gute Finanzierung würde kaum weniger als 2% Zinsen kosten. Damit bleibt fast kein Spielraum für die Tilgung des Kredits, ohne einen negativen Cashflow (also dauerhaftes monatliches Hinzuzahlen) zu produzieren.
Mit meiner Tabelle sieht das nun so aus:
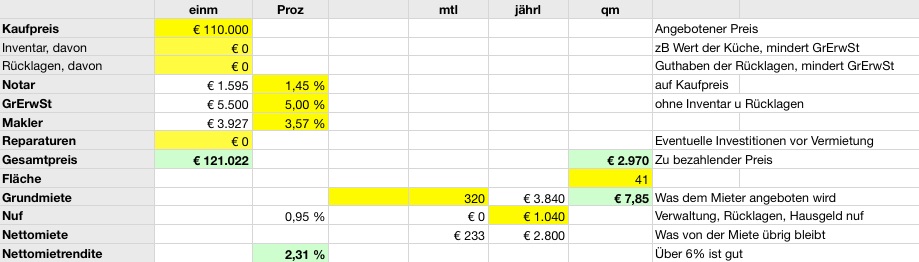
Screenshot aus meiner Immobilien-Tabelle. Du kannst sie übrigens hier downloaden.
Selbst wenn ich die 121.022 Euro von meinem Ersparten bezahlen und die Wohnung damit ohne eine Finanzierung kaufen würde, entspräche dies nur einer Verzinsung von 2,31%. Das ist mehr als man zurzeit auf dem Konto bekommt, aber es ist mir zu wenig für ein Geschäft wie den Kauf einer Immobilie.
Darum könnte man auf den ersten Blick sagen: die Immobilie ist zu teuer und darum als Renditeobjekt nicht geeignet.
Doch warum habe ich sie dennoch gekauft?
Den wichtigsten Grund habe ich schon eingangs erwähnt: durch eine Mietsteigerung lässt sich der Wert dieser Immobilie nach dem Kauf erhöhen.
Und was ist der Wert der Immobilie, könntest du dich nun fragen. Ist er nicht dasselbe wie der Kaufpreis? Nein, absolut nicht. Der Wert ist das, was man für den Kaufpreis bekommt.
Weil die Wohnung schon fast zwei Jahre lang an denselben Studenten vermietet ist, darf ich als Vermieter die Miete erhöhen. Normalerweise sind 20% Erhöhung der Nettomiete alle 3 Jahre erlaubt, doch in diesem Fall gibt es für diese Stadt eine zusätzliche Kappungsgrenze, und somit darf ich die Miete nur um 15% alle drei Jahre erhöhen.
Das ist dann aber sofort möglich (und danach eben drei Jahre lang nicht mehr).
Ich kann (und werde) also gleich nach dem Kauf der Wohnung die Miete von 320 Euro auf 368 Euro erhöhen.
Wenn ich in meiner Tabelle alles unverändert lasse und nur die Miete anpasse, dann erhöht sich die Nettomietrendite von 2,31% auf 2,79% (das ist übrigens eine Erhöhung der Rendite um fast 21%).
So geht kluges Investment
Jetzt wird die Rechnung spannend, denn nun kommt die Bank ins Spiel. Ich werde dir nun zeigen, wie es mir gelingt, mit dem Geld der Bank die Rendite meines eigenen Investments deutlich zu erhöhen.
Die Bank bietet mir einen Finanzierungskredit mit einem effektiven Jahreszins von 2%.
Ich trage also in die Tabelle ein: Zins = 2%
![]()
Die für mich nun alles entscheidende Frage ist, wie viel eigenes Geld ich einsetze, und wie viel Geld ich mir von der Bank leihe. Also die Eigenkapitalquote.
Und ich werde dir jetzt erklären, wie genau ich sie bestimme.
Zuerst lege ich fest, wie lange im Kreditvertrag die Zinsfestschreibung läuft. Also wie lange ich mich darauf verlassen kann, dass sich der Zinssatz, zu dem mir die Bank das Geld geliehen haben wird, nicht verändert. In meinem Fall nehme ich 15 Jahre.
Ich trage also in die Tabelle ein: Zinsfestschreibung = 15 Jahre.
![]()
Was noch fehlt, sind Tilgung und die Höhe des Eigenkapitals. Und diese zwei Werte trage ich erst am Schluss der Kalkulation ein.
Und dabei behalte ich immer einen Wert im Auge: den Cashflow nach Steuern. Er soll eine schwarze Null sein, also eine möglichst kleine Zahl, aber großer als Null.
![]()
Ich rechne meine Kalkulation also gewissermaßen rückwärts.
Mein Ziel ist es, dass ich nach dem Kauf nie wieder eigenes Geld in die Immobilie investieren muss. Darum muss der Cashflow größer sein als Null (denn wäre er negativ, so wäre dies das Geld, dass ich monatlich hinzuzahlen müsste).
Gleichzeitig aber ist mein zweites Ziel, dass ich nach 15 Jahren, also zum Ende der Zinsfestschreibung, den gesamten Kredit getilgt haben werde.
Das ist das Herz meiner Kalkulation.
Ich sage es nochmal in anderen Worten: in der Zeit, in der der Kreditvertrag mit der Bank unverändert läuft, also solange die Zinsfestschreibung gilt, werde ich den gesamten Kredit tilgen. Und zwar ohne eigenes Geld hinzuzahlen zu müssen.
Doch womit tilge ich dann den Kredit?
Du ahnst es:
Mein Mieter zahlt meinen Kredit zurück.
Meine Kalkulation ist nämlich genau so aufgebaut, dass ich so gut wie ohne Risiko den gesamten Kredit von den Mieteinnahmen zurückbezahlen kann.
Der Mieter zahlt den Kredit zurück
Das ist meine goldene Regel. Und sie bestimmt auch, mit wie viel Eigenkapital ich die Immobilie kaufe. Oder anders gesagt: wie viel Geld ich mir von der Bank für den Kauf leihe.
In diesem Fall sehen die Zahlen also so aus:
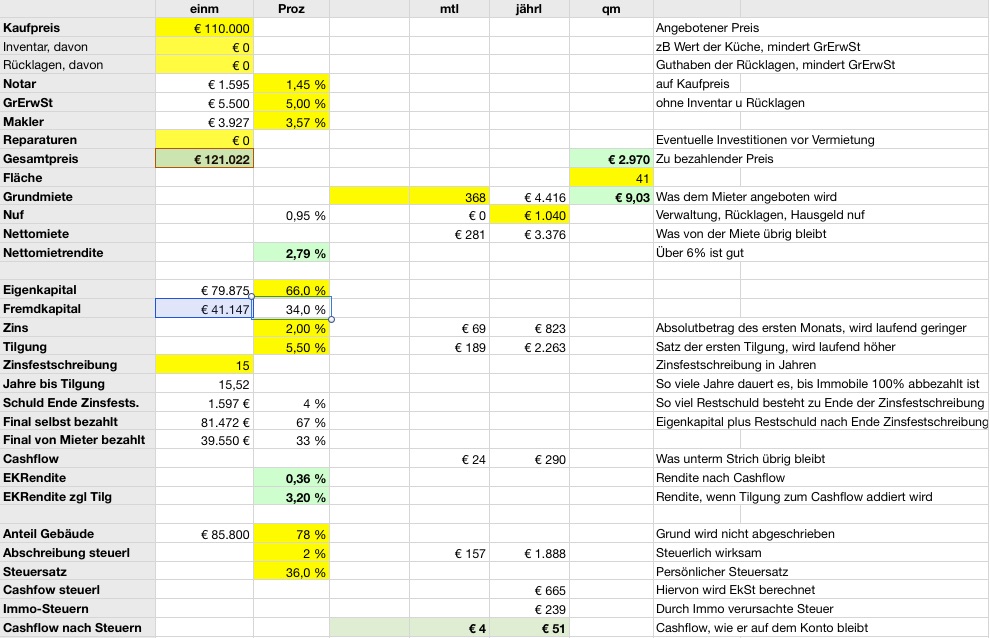
Screenshot aus meiner Immobilien-Tabelle. Du kannst sie übrigens hier downloaden.
Die oberen Zeilen haben wir ja bereits mit Inhalten gefüllt.
Eingetragen hatte ich dann:
Zins: 2%
Zinsfestschreibung: 15 Jahre
Dann habe ich die Höhe der Tilgung so festgelegt, dass ich die „Jahre bis Tilgung“ etwa bei 15 liegt.
In diesem Fall muss ich also mit 5,5% pro Jahr tilgen, damit nach den 15 Jahren so gut wie keine Restschuld mehr besteht. Hier bleiben noch 1.597 Euro Verbindlichkeiten an die Bank übrig nach 15 Jahren, aber das ist ja fast Null.
Wenn ich mit weniger als 5,5% tilgen würde, so würde die Tilgung länger als 15 Jahre dauern. Und wenn ich mit mehr als 5,5% tilgen würde, so wäre die Restschuld schon früher als nach 15 Jahren auf Null, und meine Zinsfestschreibung wäre zu lang (was nur deswegen nicht gut ist, weil die Bank dafür einen etwas höheren Zins verrechnet).
Ich liege also mit einer Tilgung von 5,5 genau richtig, und nun geht mein Blick auf den Cashflow, während ich mit der letzten wichtigen Zahl spiele: dem Eigenkapital.
In diesem Fall muss ich mindestens 66% Eigenkapital aufbringen, damit mein Cashflow nicht negativ wird. Würde ich also weniger als 79.875 Euro selbst zu dieser Immobilie beisteuern, so wäre sie 15 Jahre lang ein kleines Verlustgeschäft.
Am Ende kommt bei meiner Kalkulation also folgendes heraus:
Zins: 2% (von Bank vorgegeben)
Zinsfestschreibung: 15 Jahre (von mir verlangt)
Tilgung: 5,5% (von mir errechnet)
Eigenkapital: 79.875 Euro (von mir errechnet)
Mit diesen Zahlen habe ich mein eingesetztes Kapital von knapp 80.000 Euro zwar nur mit 3,2% Rendite verzinst (wenn ich Rendite plus Tilgung addiere). Das ist nicht die Welt, aber schonmal höher, als wenn ich die gesamte Immobilie selbst finanzieren würde und für die 121.022 Euro rechnerisch 2,79% Rendite bekäme.
Ich reduziere also mein eingesetztes Kapital und erhöhe dafür die Rendite, die ich dafür bekomme.
Im Idealfall bedeutet dies, dass ich mit demselben Geld eine größere Anzahl von Immobilien kaufen kann und dafür eine höhere Rendite bekomme (die anfangs jedoch in die Tilgung geht und erst nach 15 Jahren als Rente an mich fließt und ausgegeben werden kann).
Judo spielen mit dem Geld der Bank
Ich habe also mit dem Bank der Geld Judo gespielt und es zu meinem eigenen Vorteil genutzt. Ich leihe mir Geld, und mit dem geliehenen Geld verdiene ich Geld. Das nenne ich das Geheimnis des Kapitalismus, und ich habe diesen langen Blogpost darüber geschrieben.
Je höher die Nettomietrendite liegt, desto besser funktioniert dieses Spiel. Und im Jahr 2017 sind die Renditen für Immobilien (wie für alle anderen Kapitalanlagen) leider sehr niedrig, und darum funktioniert das Spiel jetzt auch nicht mehr ganz so gut wie noch vor wenigen Jahren (als ich die ersten Artikel darüber schrieb).
Doch in diesem Fall ist mein Vorgehen in erster Linie etwas anderes:
Ich nutze das Angebot der Bank, um mit „nur“ 79.875 Euro eine Immobilie zu kaufen. Durch den Kreditvertrag ist ein Geschäft für die kommenden 15 Jahre fixiert, und am Ende wird die Immobilie abbezahlt sein und mir gehören. Die Bank hilft mir also dabei, dass meine Mieter in den kommenden 15 Jahren 33% des Kaufpreises für mich bezahlt haben werden.
Doch nun gibt es noch zwei Faktoren, die ich bislang nur angedeutet bzw. noch gar nicht erwähnt habe. Sie helfen beide, um diesen „Deal“ noch besser zu gestalten.
Erstens wird mein Student nach knapp 2 Jahren ausziehen. Das ist bereits so vereinbart. Und danach kann ich die Wohnung neu vermieten und einen marktüblichen Preis verlangen. Das wird die Rendite massiv verbessern, ist aber kaum noch präzise zu berechnen, weil es ja erst in zwei Jahren beginnt.
Zur Abschätzung nutze ich wieder meine Tabelle. Eine marktübliche Miete heute wäre 13,50 Euro pro Quadratmeter. Oder 550 Euro Kaltmiete. Das entspricht einer Nettomietrendite von 4,59%.
Ich bräuchte dann nur 50% Eigenkapital, um mit einer solchen Mieteinnahme die Immobilie nach 15 Jahren abbezahlt zu haben. Damit wäre mein eingesetztes Kapital rechnerisch mit 7,19% verzinst, was bereits ein ordentlicher Wert ist für 2017.
In der Tabelle sieht das dann so aus:
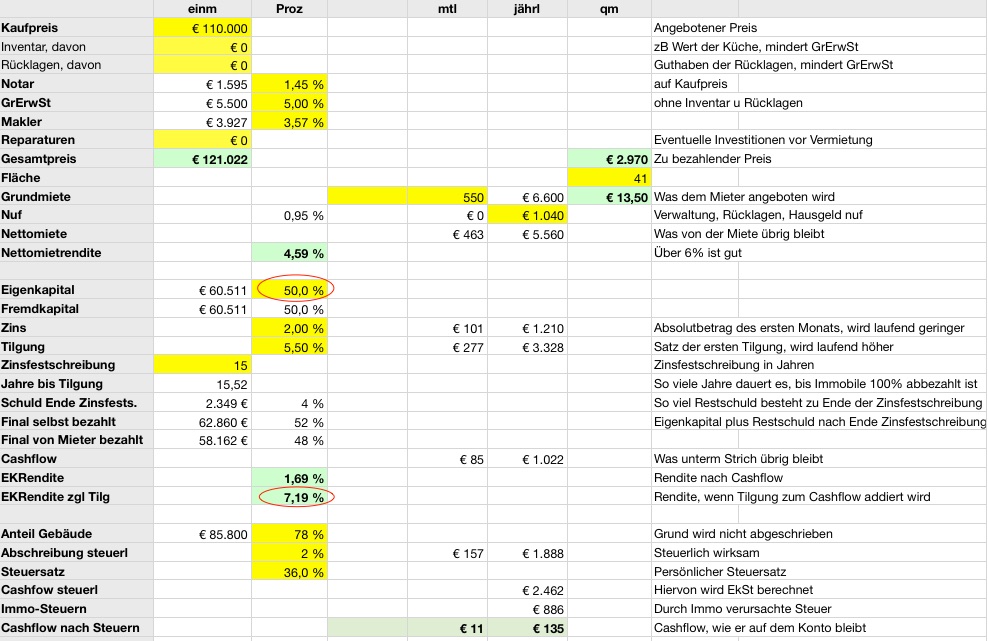
Ich werde darum die Immobilie so finanzieren, dass ich in den ersten beiden Jahren einen leicht negativen Cash-Flow habe, aber ab dem dritten Jahr nicht mehr. Somit komme ich zwar nicht kurzfristig, wohl aber nach 2 Jahren zu den genannten Zahlen. Und in der Zwischenzeit „kostet“ mich die Immobilie 105 Euro pro Monat.
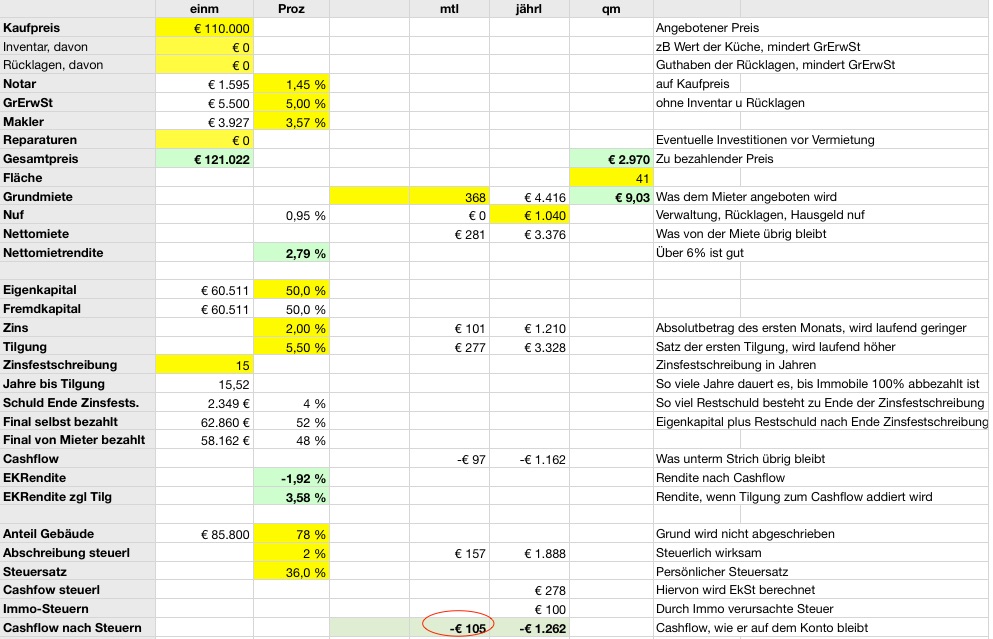
Screenshot aus meiner Immobilien-Tabelle. Du kannst sie übrigens hier downloaden.
Und der zweite Grund ist die Küche.
In der Wohnung ist eine alte Küche, und mein Mieter ist einverstanden, dass ich ihm gegen eine Mieterhöhung eine neue Küche einbauen lasse.
Das wird etwa 4.000 Euro kosten, und ich werde die Küche auf 11 Jahre abschreiben (so darf man das). Also die Miete pro Jahr um 4.000 / 11 = 364 Euro erhöhen. Das sind 30 Euro im Monat, und es entspricht einer Verzinsung der investierten 4.000 Euro von etwa 9%.
Weil die anfängliche Nettomietrendite geringer als 9% ist, erhöht sie dieses kleine Investment dann natürlich ein wenig. Die Details erspare ich euch jetzt aber. In der Tabelle trägt man diese 4.000 Euro übrigens ganz oben unter ‚“Reparatur“ ein.
Ich fasse also zusammen:
Mit diesem Kauf spekuliere ich auf keine Marktveränderung. Das ist mir ganz (ganz ganz) wichtig. Nur weil Immobilien in den letzten Jahren ständig teurer wurden und Mieten ständig stiegen, heißt das nicht, dass es auch weiterhin so ist. Es mag für die nahe Zukunft vielleicht mit einer gewissen Wahrscheinlichkeit eintreffen, aber marktbereinigende Veränderungen treten stets plötzlich und unerwartet auf.
Es wäre also fahrlässig auf eine solche Wertsteigerung zu spekulieren.
Darum rechne ich immer nur mit Werten, die mit dem heutigen Tag gelten (auch wenn ich einen davon in diesem Fall erst in zwei Jahren umsetzen werde).
Und unter diesen Voraussetzungen habe ich mithilfe meiner Rendite-Tabelle den genauen Betrag von Tilgung und Eigenkapital so optimiert, dass ich den Kredit von diesem Kauf bis zum Ende der Zinsfestschreibung komplett getilgt haben werde. Und dies (von den ersten beiden Jahren abgesehen) alleine durch die Zahlungen meines Mieters.
Hier sind alle meine Artikel über Rendite-Immobilien:
- Wie ich 40% Rendite mit Immobilien erziele.
- Rendite mit Immobilien – oder das Geheimnis des Kapitalismus (mein populärster Artikel)
- 12% Rendite mit einer Wohnung
- Rendite-Tabelle mit Handbuch (Download meiner Excel-Tabelle)
- Warum ich eine Immobilie mit 2% Rendite kaufe (diesen Artikel liest du gerade).

